Electromagnetism - Faraday’s law

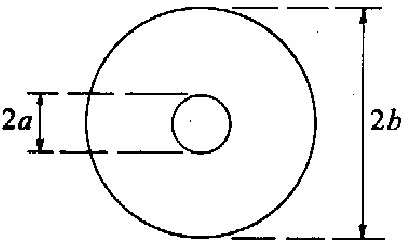
A small circular wire loop of radius a is located at the center of a much larger circular wire loop radius b as shown above. The larger loop carries an alternating current I = I₀ cos ωt, where I₀ and ω are constants. The magnetic field generated by the current in the large loop induces in the small loop an emf that is approximately equal to which of the following? (Either use mks units and let μ₀ be the permeability of free space, or use Gaussian units and let μ₀ be 4π/c².)

A.
B.
C.
D.
E.

(GR8677 #81)

Solution:

Faraday's Law: ɛ = − dΦ/dt
with  Φ = NBA  

Biot Savart Law: B ~ I

Given:
I = I₀ cos ωt → B ~ I₀ cos ωt
Area of smaller loop with radius a, A = πa²
N = 1

→ Φ = BA ≈ πa² I₀ cos ωt
→ ɛ ~ dΦ/dt ≈ πa² ω I₀ sin ωt

Only (B) fits the equation.

Answer: B


Complete Calculation:

Faraday's Law: ɛ = − dΦ/dt
with  Φ = NBA  

Magnetic field at the center of a current wire loop:  (Proof)
For the larger loop with radius b, carrying I = I₀ cos ωt →

Area of smaller loop with radius a → A = πa²

N = 1